16格智力拼图游戏解法

     16格智力拼图是一种常见的智力小游戏，将16个正方形格子排列成4x4的方阵，前15个格子分别标上数字1到15，最右下角的格子空白，然后将这些格子随机打乱，空白格子可以和上下左右的格子交换位置，要求利用空白格子将数字顺序还原。如下图所示，要求将左图还原成右图。

    这个游戏还有一个常见的变种，将一幅正方形的图片切割成4x4的16个小图片，将最右下角的格子留白，然后将这些图片打乱，要求通过空白格子将图片复原。这两种游戏的玩法完全是一样的。下面主要以数字格子来讲解这一游戏的玩法，学会了数字还原的方法，图片还原的方法自然也就会了。

    16格智力拼图游戏初一上手时往往让人无所适从，顾此失彼。不过在看完本文的讲解并做一些实际联系之后，就会发现这个游戏其实十分简单。在正式讲解之前再说几句废话。其实并不是每一种随机排列都能还原成顺序排列的。我们把能还原的排列称为有解排列。通过数学的方法证明，在所有的排列中，有解和无解排列各占一半。可以通过数学的方法判断一个排列是否有解，在本文的末尾将对判断方法做一个说明。

    好了现在言归正传。我在这里所说的方法并不是这个游戏唯一的解法，可能也不是最快的解法，但是肯定是能够解决问题的方法。整个游戏的解法中只有两个难点，掌握了这两个难点的解决方法，游戏就能很顺利地解开了。游戏的解法的大顺序是：首先还原第一行，然后还原第二行，最后还原第三和第四行。

    （1） 还原第一行

    首先将1、2、3三个格子还原。这没有任何难度，任何人稍微摸索都可以很容易做到这一步，在这里就不多说了。然后第一个难点来了，在1、2、3已经还原的情况下，如何将4还原。如下图。

    这个问题有两个解决方法。

    第一个方法如下图所示。为了看得更清楚，我把不相关的格子涂白，并将其中两个格子标记为A和B，这两个格子在需要移动，但是这两个格子上的数字是什么无所谓。

    第一步，想办法将4移动到3下面，并将空格移动到2下面，这一步应该不难做到；

    第二步，将2向下移动到空格处，将3左移到原来2的位置，将4上移到原来3的位置；

    第三步，将B左移一格，A下移一格，空出4右边的位置；

    第四步，将3和4右移，2上移。至此第一行还原完成。

    第二个方法如下图所示；具体步骤就不详细说明了。

    （2） 还原第二行

    还原第二行的方法与还原第一行的方法基本相同，不再多说了。

    （3） 还原第三、第四行的最左列

    即还原数字9和13，这是游戏解法的第二个难点。

    首先看一下9和13的位置是否下列两种情况之一：

    ——9和13位于第三行并且9紧挨在13的右侧

    ——9和13位于第四行并且9紧挨在13的左侧

    如果是这两种情况之一，则顺时针或逆时针转动第三第四行的各个格子总是可以将9和13复原的。如下图所示。

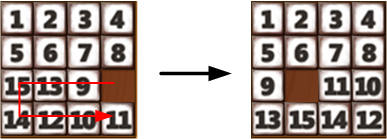
    如果9和13的位置不满足上面这两种情况，那么就需要想办法移动成这两种情况之一。方法如下：

    第一步，将13移动到第三行第一个格子，并且确保第四行第一个格子不是9或空格；

    第二步，将9移动到第三行第二个格子，这样就出现了上面的第一种情况（9和13位于第三行并且9紧挨在13的右侧）。

    只要多练习几次就能发现，上面这两步肯定是能做到的。

    （4）还原第三行和第四行的第二列

    即还原10和14，所使用的方法与还原9和13类似，不再多说。

    （5）这时就只剩下最后三个数字了，到了这个地步，很容易就能把它们放到正确的位置上。如果到这了这时发现最后三个数字不能移到正确的位置，那只可能有两个原因：一是这个排列是无解的；或者是前面的数字排列顺序有错误。

    下面谈一下判断一个排列是否有解的方法。

    （1）将各个格子（包括空白格子，其数字为16）中的数字从左至右从上至下排成一个数列，然后计算该数列的逆序和 （比较数列中任意两个数字，如果较大的数字在前则逆序和加1，用软件程序通过冒泡法很容易算出数列的逆序和）；

    （2）计算空白格子的位置到右下角的距离，如果右下角的坐标为(n,n)，空白格子所在位置坐标为（x,y)，则距离d = (n-x) + (n-y)；

    （3）如果上述逆序和与距离同为奇数或同为偶数，则排列有解，如果一奇一偶，则排列无解。

    可以简单证明一下这个方法是必要的。

    首先，游戏中的每一步其实都是移动空白格子，而完成游戏的最后一步必然是将空白格子移到右下角。因此，游戏的解决过程其实就是不断移动空白格子并最终将其移到右下角的位置的过程。容易证明，如果空白格子的初始位置与右下角的距离为偶数，则将空白格子移入右下角需要需偶数次移动；如果空白格子的初始位置与右下角的距离为奇数，则将空白格子移入右下角需要需奇数次移动。

    其次，对于数列来说，“移动”的数学解释是：假设数字16的位置为pos，则一步移动就是数字16与四个备选位置上的数字之一交换位置，这四个备选位置是pos-1、pos+1、pos-4、pos+4，容易证明，16无论与那个位置上的数字交换位置，总的逆序和增加或减少的数值都是奇数。

    综合上述两点，容易推断出上面的判断方法的必要性（但是尚未证明其充分性）。